繼續觀察漢語「嫉妒使我面目全非」，分詞後得到「嫉妒」、「使」、「我」、「面目全非」。接下來，我們試著了解這些詞是如何組成一個句子的，這樣的組成是否合乎語法，試分析其句型，「嫉妒使我面目全非」在現代漢語中屬於「使」字句，其可拆解為：

名詞・使・名詞・形容詞

或可寫成：

主語・使・賓語・形容詞。

得到句型拆解後，可以依樣造句（有如小學作業），例如：

我面目的劇變使眾人心驚膽顫

注意到主語、形容詞未必是個單詞，也可以是多詞複合，如「我面目的巨變」還可以拆解成「我」「面目」「的」「劇變」。

這代表主語作為句子的一部分並非最小單位，還可以向下拆分：

主語 = 名詞 | 形容詞・名詞 | 名詞・的・名詞 | ...

漢語有非常多句型，以下列出幾個常見的：

• 主語・動詞
  • 時光・逝去
• 主語・動詞・受詞
  • 武林盟・滅・唐門
• 主語・形容詞
  • 小明・天下無敵

想用有限句型就完全涵蓋漢語是幾乎不可能的，自然語言的語法剖析器存在於人們的腦子裡，無法強行一致，教育也只是儘量這些腦剖析器能大致相通。人的語言靈活多變，即使到了本世紀仍可能誕生新的句型、語法，而新語法誕生後，也不可能在一瞬間普及到每個人的腦子裡。學界一直在研究如何盡可能做好自然語言的剖析，雖然不可能完美，但已有許多具實用價值的成品，如中研院開發的中文剖析器線上測試，號稱能解析六萬多種句子結構，用它來剖析本文開頭的例句可得：

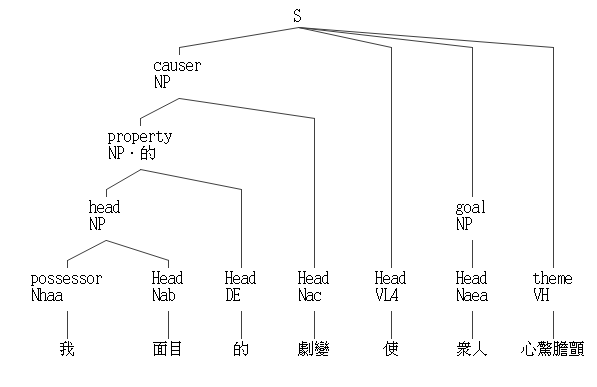
法咒的語法定義

雖然不可能讓所有人腦子裡的語法剖析器完全相同，但讓所有人電腦裡的剖析器版本相同倒是有可能的，至少版本不同的時候可以強迫用戶更新！而且法咒的語法是人造的，能在創造之初就定義好法咒的語法，而非如自然語言一般只能事後歸納。

貧道現在就來定義零・一版音界咒的語法，回到範例：

元．人數＝（１１＋３）＊４
人數＋１

音界咒只有兩種句型，一是變數宣告式，一是算式，這兩種句型可以穿插出現，其（上下文無關）語法定義可寫為：

音界咒 = 句 | 句・音界咒
句 = 變數宣告式 | 算式

第一個語法式 音界咒 = 句 | 句・音界咒 定義了一個音界咒檔案該有的樣子，它可以是 句，也可以是 句・音界咒，此處的「・」代表句之後緊接著音界咒，由於左側跟右側皆有「音界咒」，因此這是個遞迴定義，意指音界咒可分解為句・音界咒，而句・音界咒又可再分解為句・句・音界咒，一直到無窮個句・句・句・句・句...都是合法的音界咒。

語法式句 = 變數宣告式 | 算式，則近一步定義了句的樣貌，其有兩種型態，可以是變數宣告式，也可以是算式，變數宣告式很容易，只有一種可能：

變數宣告式 = "元"・"・"・變數・"＝"・算式

算式則較為複雜，敏銳的道友可能已經注意到，算式也蘊含了遞回。

算式 = 變數
    | 數字
    | "（"・算式・"）"
    | 算式・運算子・算式
運算子 = "＋" | "−" | "＊" | "／"

算式可以只是一個變數或數字，算式・運算子・算式表明算式也可以是加減乘除的結果，"（"・算式・"）"，而在算式兩側加上括號後，依然是合法括號，也就是說，１＋２是算式，而(１＋２)、((１＋２))、(((１＋２)))...也都是合法算式，０、（０）、（（０））也都合法。

思考題：有沒有辦法定義上下文無關語法，把同一層級的括號限制在一對，禁止((１＋２))、(((１＋２)))之無意義括號？

為方便觀看，以下將音界咒零・一版全部語法定義縮排後寫在一起，並加入一條音界咒檔 = 音界咒・檔案結尾，以生成檔案結尾（EOF）而完整描述音界咒檔案。

音界咒檔 = 音界咒・檔案結尾

音界咒     = 句
          | 句・音界咒

句        = 變數宣告式
          | 算式

變數宣告式 = "元"・"・"・變數・"＝"・算式

算式      = 變數
         | 數字
         | "（"・算式・"）"
         | 算式・運算子・算式

運算子    = "＋"
         | "−"
         | "＊"
         | "／"

語法歧義

前文寫出的語法定義，定義的是如何生成合乎語法的字串，而非如何將字串的語法剖析出來。

這意思是說，當吾人想生成出所有（長度小於 n）的算式時，可以遍歷算式的兩個分支得到變數宣告式、算式兩種語法，這兩種語法又可以繼續分支下去，如此遞迴，便能得出所有（長度小於 n）的算式。

但是在遞迴遍歷的過程中，不同路徑很可能會造出重複的句子。

以１＋２＊３為例，其生成方式可能是算式 => 算式＋算式 => 算式＋算式＊算式，先以＋展開，接著展開後的第二個再以＊展開，也可能是算式 => 算式＊算式 => 算式＋算式＊算式，初始算式先以＊展開，展開後的第二個算式再以＋展開，如圖：

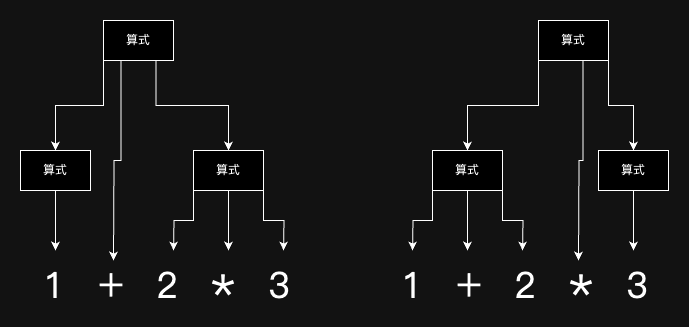
一種語法出現不同展開過程但同結果這種情況，該語法就是「有歧義的」，亦有人稱「模糊」、「模稜兩可」、「二義性」。

歧義是一項不良性質，若對上圖中得到的兩棵語法樹做後序運算求值，所得將會不相同，一個是先乘除後加減，另個則是先加減後乘除。

即使語法存在歧義，還是有辦法剖析的，舉個例子，透過回溯來得到所有可能的語法樹，再依照某種方式挑選，如此還是能用一套算法總是從一套源碼中得到相同的語法樹。

遇到歧義與法時，也可以嘗試直接修原語法定義，寫出一套無歧義的語法。算式的例子可以透過額外增加乘除式、原子式兩層級來迫使先乘除後加減：

算式   = 乘除式
      | 算式・＋・乘除式
      | 算式・−・乘除式
乘除式 = 原子式
      | 乘除式・＊・原子式
      | 乘除式・／・原子式
原子式 = 數字
      | 變數
      | "（"・算式・"）"

回溯剖析

再整理一次音界咒語法。

音界咒檔 = 音界咒・檔案結尾

音界咒     = 句
          | 句・音界咒

句        = 變數宣告式
          | 算式

變數宣告式 = "元"・"・"・變數・"＝"・算式

算式   = 乘除式
      | 算式・＋・乘除式
      | 算式・−・乘除式

乘除式 = 原子式
      | 乘除式・＊・原子式
      | 乘除式・／・原子式

原子式 = 數字
      | 變數
      | "（"・算式・"）"

前文提到，有了語法規則定義，就能透過遞迴展開生成符（生成符，即在語法規則左側出現，還能繼續展開的符號），最終獲得所有長度小於 n 的展開式。

當吾人想要剖析時，也能利用這個想法，若一份文本長度為 n ，那遞迴生成出所有長度等於 n 的展開式，並一一與原始碼做比對，比到一種展開是一模一樣的，檢視當下的展開過程，就能得到語法樹了。

一直展開到長度 n 才比對，太浪費時間了，一發現當下的展開式已經跟文本不一樣，就可以放棄目前展開，回溯到上個還沒失敗的狀態。

寫成虛擬碼如下：

// 「剖析」函式嘗試以「展開式」來生成「文本」

「文本」為一全域變數

剖析（展開式）-> 成功｜失敗：
    匹配展開式與文本，若相等，回傳成功

    首生成符 = 展開式中的第一個生成符
    
    遍歷首生成符的「生成規則」 {
        新展開式 = 在原展開式中，以「生成規則」展開首生成符
        若「新展開式」的前綴已與文本不同，嘗試下個規則

        若「剖析（新展開式）」成功，回傳成功
    }

    走到這裡表示所有規則都不行，回傳失敗

// 初始展開式僅為「音界咒檔」
剖析（音界咒檔）

以上虛擬碼為求簡單，省略了許多優化，例如說，首生成符的位置跟目前比對無誤的文本位置都應該紀錄起來，不用每次都從頭比對。另外，編譯器應用中，剖析應回傳語法樹，而非單單成功或失敗。

消除左遞迴

注意到剖析（展開式）是遞迴函式，它會嘗試以各種規則展開首生成符，然後繼繻呼叫剖析（新展開式）。

觀察剖析（算式），只要第一個規則算式 = 乘除式 配對失敗，就會嘗試匹配算式 = 算式・＋・乘除式，也就是呼叫剖析（算式・＋・乘除式），此一規則並沒有消耗任何文本，第一個規則剛剛不能生效，此刻一樣不能生效，於是會再套用一次算式 = 算式・＋・乘除式得到剖析（算式・＋・乘除式・＋・乘除式）......如此落入無窮遞迴。

若保證每個展開都能消耗掉至少一個字符，就能避免落入遞迴，但文本卻完全不變的狀況。再次改寫算式：

其中 e 代表空字串。

算式      = 乘除式・重複乘除式

重複乘除式 = ＋・乘除式・重複乘除式
          | −・乘除式・重複乘除式
          | e

乘除式    = 原子式・重複原子式

重複原子式 = ＊・原子式・重複原子式
         | ／・原子式・重複原子式
         | e

原子式    = 數字
         | 變數
         | "（"・算式・"）"

算式被改寫了真多次，由此可見寫出易於剖析的語法不是一件易事。所幸，這是零・一版最後一次重寫語法了。

零・一版語法規則整理如下：

音界咒檔 = 音界咒・檔案結尾

音界咒     = 句
          | 句・音界咒

句        = 變數宣告式
          | 算式

變數宣告式 = "元"・"・"・變數・"＝"・算式

算式      = 乘除式・重複乘除式

重複乘除式 = ＋・乘除式・重複乘除式
          | −・乘除式・重複乘除式
          | e

乘除式    = 原子式・重複原子式

重複原子式 = ＊・原子式・重複原子式
         | ／・原子式・重複原子式
         | e

原子式    = 數字
         | 變數
         | "（"・算式・"）"

抽象語法樹

依照回溯剖析算法（或是其他剖析算法），吾人能得到一棵紀錄了所有生成符展開點的語法樹。然而，語法樹中的許多細節並無實際意義。

以變數宣告式為例，元・甲＝（１），若嚴格按照展開規則，會得到如下繁複的語法樹：

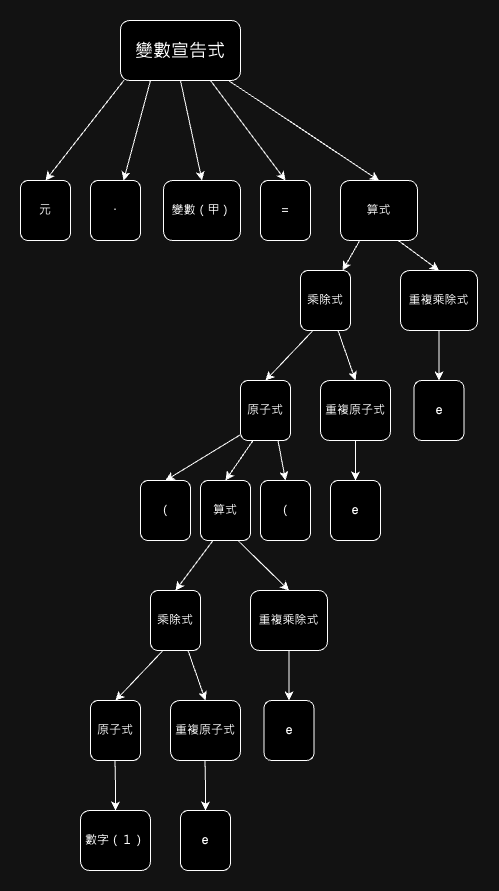
這種嚴格按照語法規則展開的語法樹，吾人稱其為「具體語法樹」，然而，具體語法樹中，某些節點含有的資訊對接下來的編譯器後端毫無用處，例如元、・、＝這些協助詞法分隔的符號，在任何變數宣告式裡都有，所以沒有紀錄的意義。另外，以如此深的樹來紀錄（１）這個算式也是極度冗餘的，原子式、重複原子式...這些玩意兒完全是為了消除左遞迴跟歧義才製造出來的，語義上僅需知道它是數字１就夠了。

省略不重要的資訊後，可以得到：

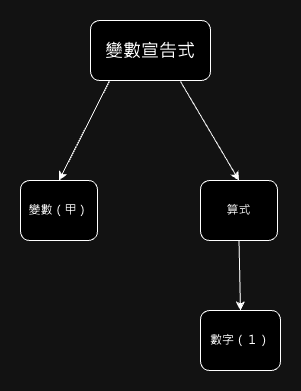
這種精簡後，但在語義上沒有損失的語法樹，被稱為抽象語法樹。若語境明確，也可以直接叫語法樹。

實作：手寫遞迴下降

先定義剖析器的輸出——抽象語法樹節點的型別。

抽象語法樹節點型別定義

pub type Ｏ語法樹 = Ｏ咒;

pub struct Ｏ咒 {
    句: Vec<Ｏ句>,
}

enum Ｏ句 {
    變數宣告(Ｏ變數宣告),
    算式(Ｏ算式),
}

struct Ｏ變數宣告 {
    變數名: String,
    算式: Ｏ算式,
}

enum Ｏ算式 {
    變數(String),
    數字(i64),
    二元運算(Ｏ二元運算),
}

struct Ｏ二元運算 {
    運算子: Ｏ運算子,
    左: Box<Ｏ算式>,
    右: Box<Ｏ算式>,
}

剖析

貧道將每個生成符規則對應到一個剖析函式，剖析函式會從詞陣列的某個位置開始，嘗試找出其對應生成符的一組展開式。

剖析函式有以下形式：

// 游標是一個索引，指到當前詞陣列尚未被剖析的最前位置
// 應用任何一條規則剖析成功時，回傳 Some(Ｏ語法樹節點)
// 所有規則都剖析不了 XXX 生成符時，回傳 None
fn 剖析XXX(&self, 游標) -> Option<Ｏ語法樹節點, 剖析後的游標位置(usize)>

先來看個簡單例子，句的剖析，句應對到兩條簡單規則

// 句        = 變數宣告式
//           | 算式

fn 剖析句(&self, 游標: usize) -> Option<(Ｏ句, usize)> {
    // 句 = 變數宣告式
    // 若匹配`變數宣告`成功，返回對應語法樹節點
    if let Some((變數宣告, 游標)) = self.剖析變數宣告(游標) {
        return Some((Ｏ句::變數宣告(變數宣告), 游標));
    }

    // 句 = 算式
    // 若匹配`算式`成功，返回對應語法樹節點
    if let Some((算式, 游標)) = self.剖析算式(游標) {
        return Some((Ｏ句::算式(算式), 游標));
    }

    // 所有規則都無法剖析，返回 None
    None
}

再來看另一個例子，變數宣告的剖析，變數宣告只對應一條規則，但是，這條規則需要匹配多個符。

// 變數宣告式 = "元"・"・"・變數・"＝"・算式
fn 剖析變數宣告(&self, 游標: usize) -> Option<(Ｏ變數宣告, usize)> {
    let 游標 = self.消耗(游標, Ｏ詞::元)?;     // 若匹配不了 "元" ，短路返回 None
    let 游標 = self.消耗(游標, Ｏ詞::音界)?;   // 若匹配不了 "・" ，短路返回 None
    let (變數名, 游標) = self.剖析變數(游標)?; // 若匹配不了 變數 ，短路返回 None
    let 游標 = self.消耗(游標, Ｏ詞::等號)?;  // 若匹配不了 "＝" ，短路返回 None
    let (算式, 游標) = self.剖析算式(游標)?;  // 若匹配不了 算式 ，短路返回 None

    Some((Ｏ變數宣告 { 算式, 變數名 }, 游標))
}

觀察這兩個剖析函式，可以發現它們的短路規則截然相反

• 剖析句分成兩個主要if區塊，當剖析成功，得到 Some 時短路返回語法樹節點。
  • 應對的是兩條展開規則，一條展開能匹配詞流就算成功
  • 稱此結構為「或」
• 剖析變數宣告則連續調用了 5 次剖析函式 （消耗也是種剖析函式，只是它特別簡單），在剖析失敗，得到 None 時短路返回 None。
  • 應對的是：詞流必須完整匹配整條展開式才算匹配成功，一項不匹配就是失敗。
  • 但 Rust 提供了 ? 語法糖，所以不用一直 if let 才能知道是不是 Some
  • 稱此結構為「且」

語法展開也不外乎這兩個結構，一個在語法規則裡用 | 來表示「或」，用 ・ 來表示「且」。

來看個「或」、「且」結構都用上的語法規則原子式，其實作不外乎這兩種結構的組合。

// 原子式    = 數字
//         | 變數
//         | "（"・算式・"）"
fn 剖析原子式(&self, 游標: usize) -> Option<(Ｏ算式, usize)> {
    // 原子式 = 數字
    if let Some((數字, 游標)) = self.剖析數字(游標) {
        return Some((Ｏ算式::數字(數字), 游標));
    }
    // 原子式 = 變數
    if let Some((變數, 游標)) = self.剖析變數(游標) {
        return Some((Ｏ算式::變數(變數), 游標));
    }
    // 原子式 = （算式）
    // 此處用上了閉包來讓 ? 語法糖生效
    // 也可以選擇多寫一個函式來專門生成`原子式 = （算式）`
    if let Some(結果) = (|| -> Option<(Ｏ算式, usize)> {
        let 游標 = self.消耗(游標, Ｏ詞::左括號)?;
        let (算式, 游標) = self.剖析算式(游標)?;
        let 游標 = self.消耗(游標, Ｏ詞::右括號)?;
        Some((算式, 游標))
    })() {
        return Some(結果);
    }
    None
}

其他規則基本按照這兩結構依樣畫葫蘆就行，但重複原子式、重複乘除式需要額外處理左結合的問題，用遞迴來寫比較冗長麻煩（尤其 Rust 還要處理所有權），但其實形如：

算式      = 乘除式・重複乘除式

重複乘除式 = ＋・重複乘除式
         | −・重複乘除式
         | e

用如下形式表示更加簡單，期中的 (x)* 表示 x 可重複零或多次：

算式      = 乘除式・(＋・乘除式)*
         | 乘除式・(−・乘除式)*

在實作中用一個 while 迴圈就能輕鬆實作：

fn 剖析算式(&self, 游標: usize) -> Option<(Ｏ算式, usize)> {
    let (mut 算式, mut 游標) = self.剖析乘除式(游標)?;
    while let Some((運算子, 新游標)) = self.消耗加減(游標) {
        let (右算元, 新游標) = self.剖析乘除式(新游標)?;

        算式 = Ｏ算式::二元運算(Ｏ二元運算 {
            左: Box::new(算式),
            右: Box::new(右算元),
            運算子,
        });
        游標 = 新游標
    }
    Some((算式, 游標))
}

音界咒的 9 條語法展開規則都寫成函式後，就可以調用

剖析咒(0)

來得到整棵語法樹了。注意到，本剖析器第一個呼叫的 剖析咒() 是語法樹最頂層的規則，它自頂向下的建構語法樹，因此吾人目前採用的回溯算法可說是一種「自頂向下」的剖析算法。

「自頂向下」剖析有很多種實作方法，如前文的虛擬碼比較像是對每條規則建表，最後再寫一個函式根據表格遞迴呼叫以完成剖析。而給每一個規則都寫一份對應函式的實作法，就被稱為「遞迴下降剖析」，大約是要強調手寫的遞迴函式互相呼叫、越來越深吧。建表法就未必要用遞迴來做，可以用棧（堆疊）來模擬。

每條規則都是手寫的雖然容易有誤，但也有靈活這個優點，除錯時想打印什麼訊息直接加在函式裡就行。從具體語法樹轉換成抽象語法樹也特別好寫，例如前面剖析變數宣告的函式，很輕鬆的就只從 5 個具體語法樹節點取出 2 個有用的抽象語法樹節點。